SCIENTIFICAMERICAN | Math
Why This Great Mathematician Wanted a Heptadecagon on His Tombstone
这位伟大数学家为何希望在他的墓碑上刻上一个十七边形
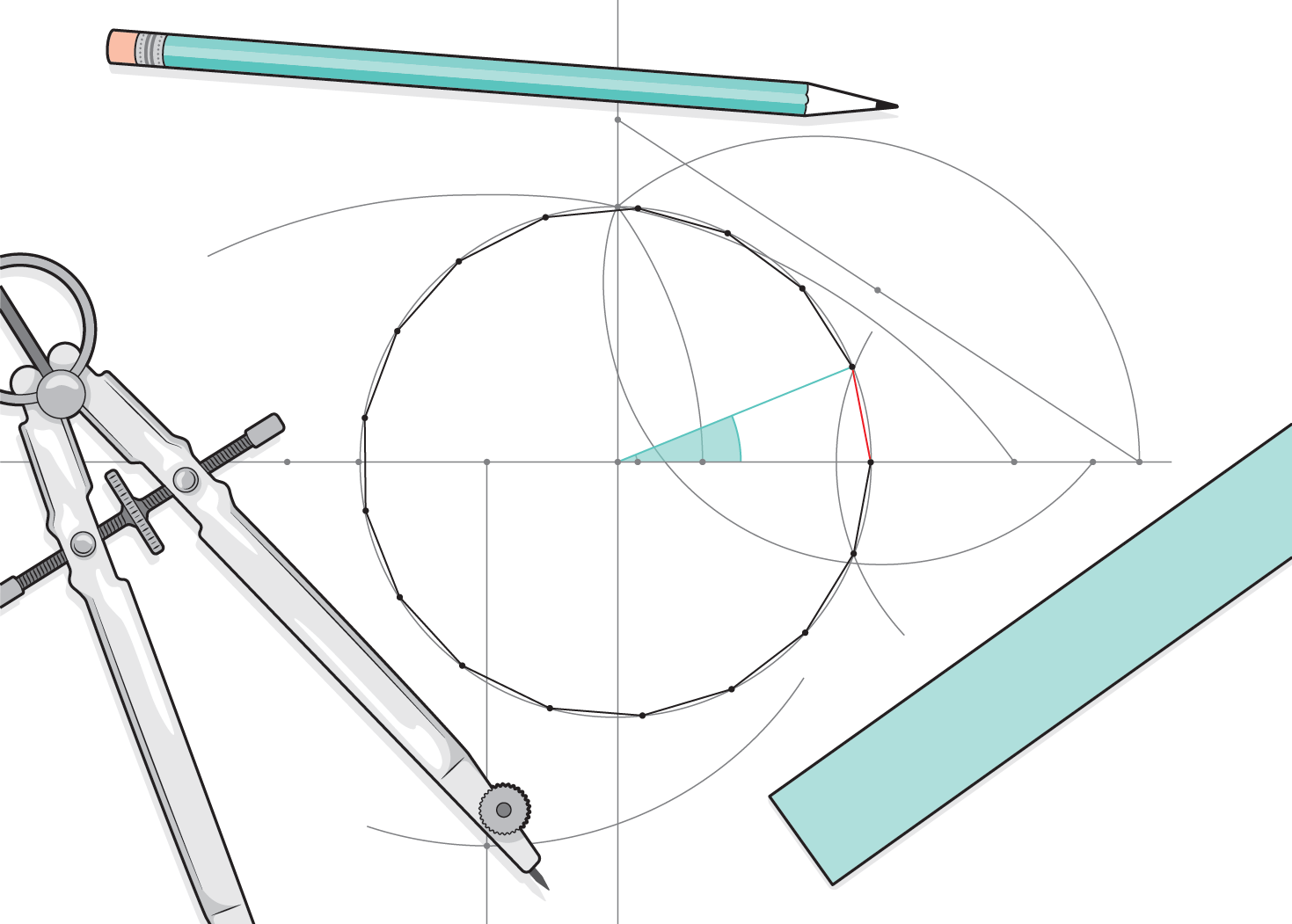
Illustration shows a compass, straightedge and pencil laid over a drawing of a 17-sided regular polygon with pencil marks showing how the shape was constructed using the tools shown.
2024-10-11 1456词 困难
The Greeks didn’t impose arbitrary rules just to make math more challenging. The game of constructing shapes with a compass and straightedge originates in Euclid’s Elements from the third century B.C.E., one of the most important textbooks ever written. Like modern mathematicians, Euclid set out to derive all of geometry from a minimal list of assumptions. Instead of merely asserting the existence of shapes or other geometric objects, Euclid wanted to build them explicitly from the simplest ingredients: lines and circles. To get a feel for these constructions, try one for yourself: find the midpoint of the line segment from A to B below. Eyeballing won’t suffice; your method must identify the exact midpoint.
免责声明:本文来自网络公开资料,仅供学习交流,其观点和倾向不代表本站立场。